Load Incremental Schemes
It describes the solution method for control of load increment size. There are five methods to be selected.
Newton-Raphson (Constant Load) Method
Single Displacement Control Method
Minimum Residual Displacement Method
Arc Length Method
Constant Work Method
Iterative Schemes
It describes the solution method for control of iterative scheme. Same as above are five methods to be selected.
Newton-Raphson (Constant Load) Method
Single Displacement Control Method
Minimum Residual Displacement Method
Arc Length Method
Constant Work Method
Incremental-Iterative Schemes
Generally the numerical methods for incremental-iterative procedure can be any methods mentioned above. For easy use, three common combinations are provided.
Newton-Raphson (Constant Load) Method
For constant load increment method, the Newton-Raphson method will be used for load incremental scheme and iterative scheme.
Single Displacement Control (Constant Displacement) Method
For constant displacement increment method, single displacement control method will be used for load incremental scheme and iterative scheme.
Arc Length Method + Minimum Residual Displacement Method
Arclength method will be used for load incremental scheme and minimum residual displacement method will be used for iterative scheme.
Solution Methods
Newton-Raphson (Constant Load) Method
This is the only method providing the response of a structure at the input load in terms of buckling strength and therefore it should be used check the adequacy of a structure under a set of factored design loads. In the Newton-Raphson method, iteration is activated to obtain the equilibrium condition between the applied forces and the internal structural resistance within a load step. Unlike the pure incremental method in which no equilibrium check is performed, the unbalanced force is dissipated via the iterative procedure and can therefore be eliminated by this method. Being free from the drift-off error, the solution is more accurate and the computational time is reduced when compared to the pure incremental method. The general procedures can be summarized in Figure1 and Figure2.
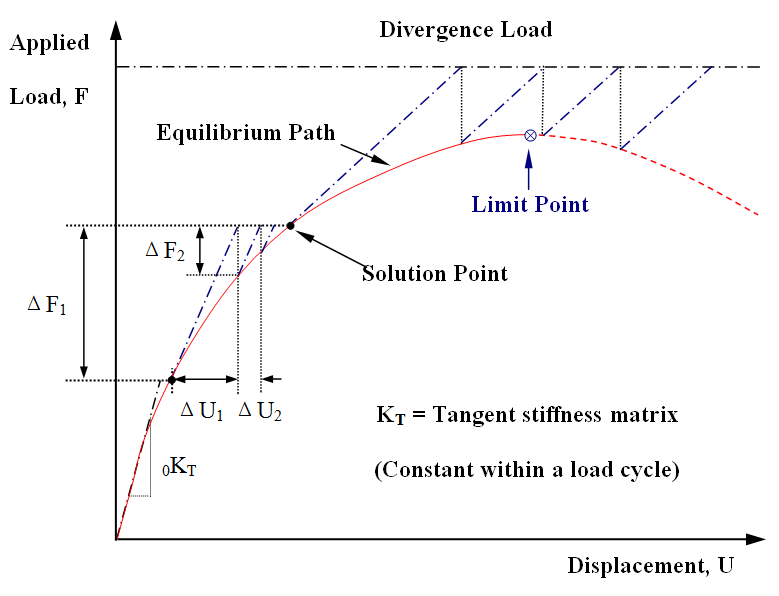
Figure1 Conventional Newton-Raphson Method

Figure2 Modified Newton-Raphson Method
For the conventional Newton-Raphson method, the tangent stiffness matrix of the structure will be updated at every iteration while for the modified Newton-Raphson method, it is reformed only in the first iteration and is kept unchanged within the load cycle.
The conventional and the modified Newton-Raphson methods usually provide a rapid rate of convergence in the stable equilibrium range. However, when approaching the limit point of the load-deflection curve, a large number of iterations will be required even for a small load increment. In the Newton-Raphson method, the solution point at the specified applied load level is sought and therefore any unloading path cannot be traced. Consequently, the solution scheme diverges near the critical point due to the ill-conditioning of the tangent stiffness matrix or simply due to the size of the load increment being greater than the limit load as shown above.
Single Displacement Control Method
Unlike the load control methods previously described, a constraint equation for displacement is imposed in this approach. The displacement control method was originally proposed by Argyris (1965). In his study, however, the symmetrical nature of the tangent stiffness matrix is destroyed by adding the displacement constraint equation. In order to retain the symmetrical property of the tangent stiffness matrix, Batoz and Dhatt (1979) imposed the constraint for displacement via iteration. According to their procedure, a single displacement degree of freedom is chosen to be constrained.
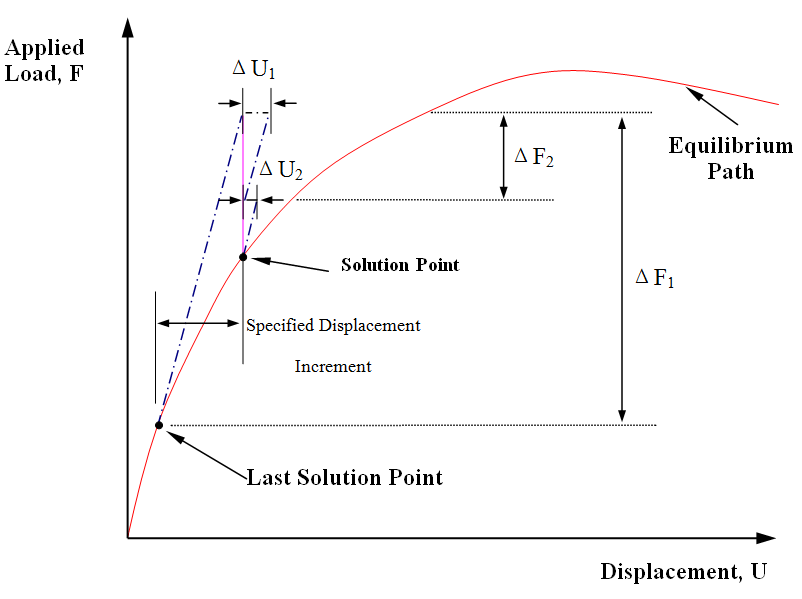
Figure3 Displacement Control Method
The diagrammatic presentation of the procedures is depicted in Figure3. The constant displacement method does not exhibit any difficulty in passing the snap-through limit point but fails to converge in snap-back problems. Thus, it is usually used in conjunction with other solution schemes in order to solve general nonlinear problems. For example, Sabir and Lock (1972) used the constant load Newton-Raphson method, which can handle the snap-back but not the snap-through problem, together with the constant displacement method in their nonlinear analysis of shell structures exhibiting snap-through and snap-back behaviour.
Constant Work Method
Similar to the constant displacement method, the basic idea of the constant work method is to impose a constraint equation to guide the incremental load. In this case, the work done by the external loading is kept constant within a load increment. The use of this concept on nonlinear analysis has been reported by many researchers including Honecher (1980), Powell and Simons (1981), Karamanlidis et al. (1981), Bathe and Dvorkin (1983) and Yang (1984).
Graphical illustration of the procedure for the constant work method is shown in Figure4. It can be seen from the figure that the load increment is directed towards the load-deformation curve so that there would not be any difficulty in handling both general snap-through and snap-back problems. Exception of this will be the case when the loaded degrees of freedoms exhibit snap-back behaviour. This characteristic has been discussed by Chan and Ho (1990). However, Bathe and Dvorkin (1983) showed that its rate of convergence is slow when compared to the arc-length method which is discussed in the following sub-section.
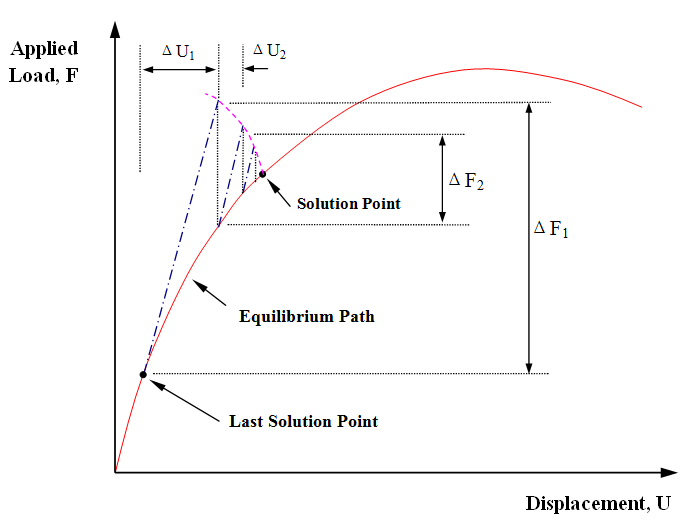
Figure4 Constant Work Method
Arc Length Method
Different forms of the arc-length method have been proposed by Wempner (1971), Riks (1979) and Ramm (1980, 1981) for nonlinear analysis. In NIDA, the spherical constant arc-length method suggested by Crisfield (1981) is adopted as it shows to be more reliable than others.The basic concept of the spherical arc-length method is to constrain the load increment so that the dot product of displacement along the iteration path remains constantly in the 2-dimensional plane of load versus deformation.
It is noted that the sign for the load increment will be the same as that for the determinant of the updated tangent stiffness matrix. In other words, a positive determinant will lead to an increase in loading while a negative determinant will result in a decreasing load. This concept of choosing the sign was first suggested by Bergan and Soreide (1978) in their studies using the method of current stiffness parameter.
The procedure of the spherical arc-length method is illustrated in Figure5. Owing to its accuracy, reliability and satisfactory rate of convergence, it is probably the most popular method for nonlinear analysis and it was noted to be robust and stable for pre- and post-buckling analysis.
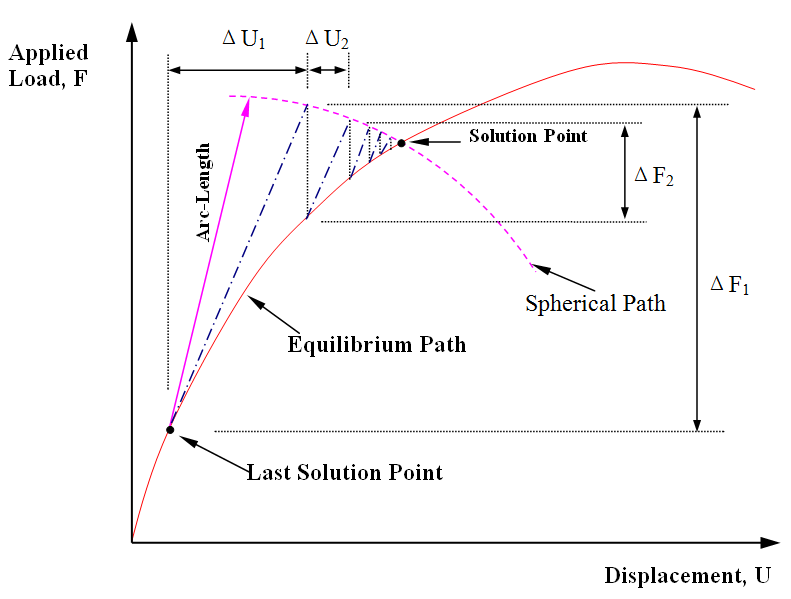
Figure5 Arc-length Method
Minimum Residual Displacement Method
The basic idea of this method originally proposed by Chan (1988) is to minimize the norm of residual displacement in each iteration. The graphical representation of the procedure is demonstrated in Figure6. From the figure, it can be seen that this constraint condition enforces the iteration path to follow a path normal to the load-deformation curve. It adopts the shortest path to arrive at the solution path by error minimization and thus is considered to be an optimum solution. In addition, the procedure is much simpler to use than the arc-length method. Generally speaking, owing to its efficiency and effectiveness in tracing the equilibrium path, the minimum residual displacement method is usually chosen to perform the iterative procedure and combined with the part for load size determination in the first iteration by the arc-length method. Unless otherwise specified, the combination for the nonlinear solution strategy is used in NIDA for static analysis.
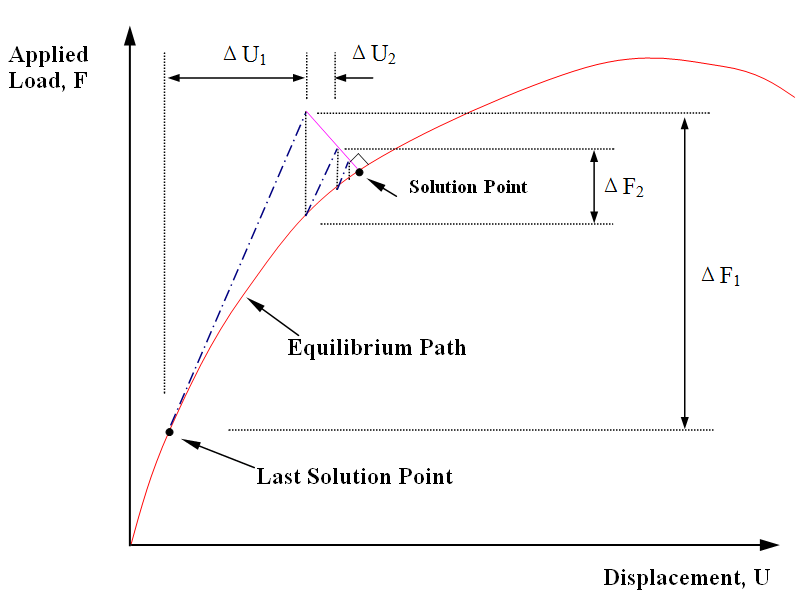
Figure6 Minimum Residual Displacement Method
