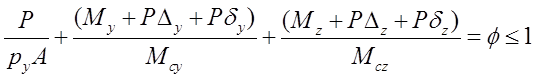Background of Second-Order Analysis
Nida checks the section capacity along the length of every initially curved member for P-δ effect, which is required by design code for member imperfection and member second-order effect. Other software only check the P-Δ effect at element ends which is inadequate for full second-order analysis. As the P-Δ and the P-δ effects have been considered in Nida, no effective length or λcr factor is required to be determined.
The following second-order effects, which are required by most national design codes of practice, have been included in calculation of member forces and checking of member and system design strength, via a second-order analysis procedure.
Figure1 The type "A" tested frame used for present studies
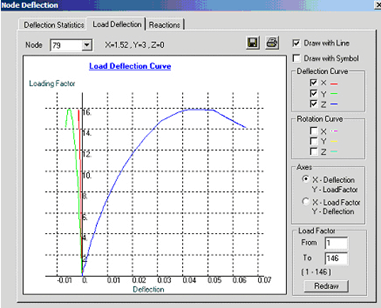
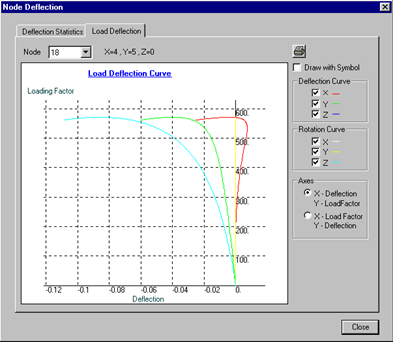
Figure2 Load vs deflection curve for imperfection of 0.5% of scaffold height
- The effect of member slenderness (Le/r) on the axial force capacity of a column and a strut.
- The change of member stiffness due to the presence of axial force. In other words, a member stiffness under axial compression will be reduced and it is accounted for in the analysis. For example, the compressive bracing member takes a much smaller load than the tensile bracing member. This checking will be required by some design codes that the effectiveness of a restraining member when under force should be considered.
- The effective length ratio (Le /L) or K-factor is automatically allowed for in the analysis and thus its assumption is not needed. No assumption or evaluation of effective length is required. Thus, the classification of sway and non-sway frames for determination of effective length ratio as required by some ultimate limit state design codes (e.g. BS59501) is not needed. Note that effective length can hardly be assessed accurately in many real cases.
- The global structural instability such as snap-through buckling, additional moment due to sway and P-Δ effects are considered in the incremental-iterative second-order analysis procedure.
- Reserve in strength after yielding can be explored with the second-order plastic Analysis.
The design and buckling capacity of a structure can be computed by incrementing the loads until member failure, sensed by material yield or excess of sectional strength as
Eurocode and new LFRD advise us to use second-order analysis. BS5950(2000) advises us not to use the first-order linear analysis for slender frames in clause 2.4.2.7 as "If lcr is less than 4.0, second-order analysis should be used". Are we sure our structures will not have a lcr less than 4 and, shouldn't we use second-order analysis which is applicable to any value of lcr and will always give us a safer and a more economical design ? Euro code-III has also been recommending engineers in using second-order analysis. Are we behind in this race of technology ?
Are we or our engineers equipped with this better and new design method recommended in national design codes in most countries with advanced technology ? Please spend a few minutes to check the following.
If we do not want our structures to failure before reaching the design loads, we or our engineers should at least be able to determine whether or not the following simple frame has the design strength to take a pair of point loads of 100 tons and 50 tons at its tops, coming from a point load of 150 tons at one third bay distance from one column top. One case is tied at top and the other case is not tied.
All columns : 203x203x60UC bent about minor axis : A = 7640 mm2. I=2.0x107mm4, Z=1.99x105mm3
Others : 152x152x37 UC bent about major axis : A = 4730 mm2. I=2.2x107mm4, Z=2.74x105mm3
All steel grade S355.
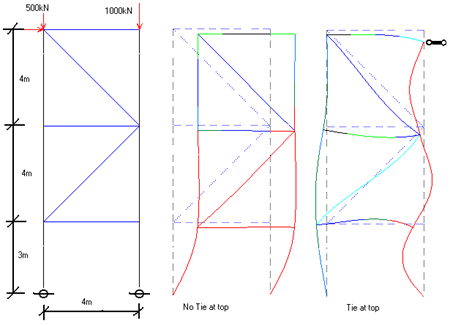
Our solutions are 126 tons for "no-tie" case and 207 tons for "tie" case (total load). Colour on each member of the frame on last page shows its design strength check.
Can your currently used software solve the problem in comply with the design code quickly ? If not, please consider using one which is capable of doing the second-order analysis with section capacity check to improve your competitiveness and safety of your design.

A scaffolding system designed and analysis safely in Taiwan by Nida without using the code for member strength check and assumption of effective length. The design is completed within a few minutes.
Both frames below have elastic critical load factors lcr less than 10 and larger than 4 and therefore their column use the same design chart in Appendix E of BS5950 (2000) for unbraced or sway frames. After reading the following large deflection plot, do you think they really behave similarly under the same set of increasing loads ?
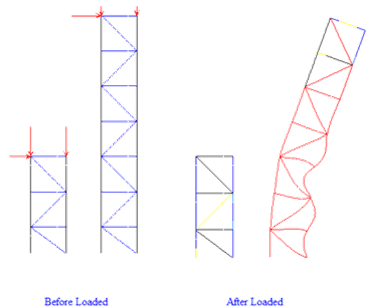
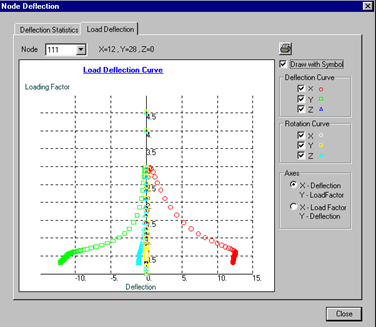
Figure3 Load deflection paths of node at top of taller frame