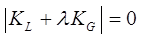Background
In structural analysis and design, a suitable model to represent and simulate the true behaviour of a structure is necessary for obtaining an accurate output. The first-order linear analysis is based on the
assumption of elastic material behaviour and undeformed structural geometry for equilibrium check.The elastic analysis does not fully comply with the requirements of the limit state design (LSD) philosophy and additional member check is needed to ensure nonlinear effects due to buckling and plastic failure do not occur under the design loads. Also, the use of plastic moment capacity in design and the adoption of an elastic analysis are inconsistent. More critically, buckling is system behaviour while the design check is member-based and they are not compatible with great uncertainty in effective length factor (Le/L).
A complete non-linear analysis traces the structural response until the limit state is reached with allowance for non-linear geometrical and material behaviour and imperfections. As such, the limit load from the analysis can be directly compared with the factored design load and individual member design becomes unnecessary. Because of this characteristic, the method is sometimes called the “Direct analysis” in the U.S.A. However, in order to simplify the complexity of an analysis, different versions of non-linear analysis are available. The engineer must therefore fully realize the limitation of any one of these versions otherwise disaster due to over-estimation of load resistance may occur. The P-Δ-only version of second-order analysis requires additional checks using the tables in the code and the software is not fully “automatic”. All software for second-order non-linear analysis, like the first-order linear analysis, requires careful input of data file and interpretation of data output. This section introduces the design concept for a second-order elastic and plastic analysis of steel frames used in many real projects. Below is a summary of these methods which are essential in understanding the new design theory.
First-order Linear Analysis
As other structural analysis software, NIDA plots the bending moment and shear force diagrams under the assumption that change in geometry under load does not affect the structural stiffness.
Second-order Analysis
In this second-order analysis, NIDA performs the following functions.
- Calculate the displacements and rotations at all the nodes or junctions of elements or members, allowing for the change of structural geometry (P-d and P-D effects) upon loading.
- Calculate the bending moments about the element cross sectional axes, torsional moment about the longitudinal axis and axial force in the member, allowing for the second-order non-linear effects due to axial force. Shear will also be determined in the computer output.
- Design a structure by section capacity check that effective length is not required to be assumed.
- Check the instability of members as well as global structure.
- Design the structure by a system approach, in contrast to the traditional “member-based” design method.
Second-order Elastic Analysis
In the design of steel structures by second-order non-linear analysis, the program increments the load in a step-by-step and incremental-iterative manner. Thus, a small increment of, say, from 5 to 25%, of expected design load is applied to the structure and the displacements are then computed and used to calculate the resistance. Iteration for equilibrium is carried out if they do not balance and convergence is assumed when the error of the norm of the unbalanced forces is smaller than 0.1% of the applied force. After convergence, the section capacity is checked for each member using Equation below. When any one of the members fails to meet the section capacity check, it is considered to have failed and it is then indicated in red and shown in post-viewer. After this step, a new load increment is applied and the same iterative procedure is exercised. This incremental-iterative procedure is activated until the specified number of load increments has been applied and the analysis is completed or when divergence occurs. In the whole design and analysis process, no assumption of effective length is needed since the P-d and P-D effects have been considered in Equation below.
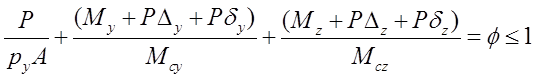
Second-order Plastic Analysis or Advanced Analysis
This type of second-order plastic or advanced analysis is similar to the above elastic analysis except it needs not stop at the first plastic hinge as its design resistant load. When a member fails, a hinge is inserted to the member end close to the hinge position and analysis continues until the collapse load is reached. The collapse load is taken as the load level which does not allow further load increase indicated as a curve reaches plateau, descends or stagnates in the load vs. deflection plot. In design, this collapse load should be greater than or equal to the factored design load in all load cases.
In Plastic Advanced “plastic element” analysis, when a member reaches its design resistance, the axial force and moments of the member are kept constant and not allowed to change with the increasing load. This implies additional loads will be re-distributed to other members.
In plastic advanced “plastic hinge” analysis, when a member reaches its design resistance, a plastic hinge will be inserted to the node close to the location of plastic moment.
Note that, in second-order elastic-plastic analysis, the load increment should be smaller and generally should be less than 1% of the expected design load. Also, the arc length plus minimum residual displacement method should be used with control parameters sufficiently smaller, normally between 2 to 3.
Vibration and Buckling Analysis
NIDA determines the natural frequency by lump mass or consistent mass assumptions and the eigen-value buckling load factor as follows.
- For natural frequency analysis
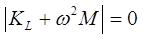 and
and 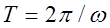
- For eigenvalue buckling analysis